11053번: 가장 긴 증가하는 부분 수열
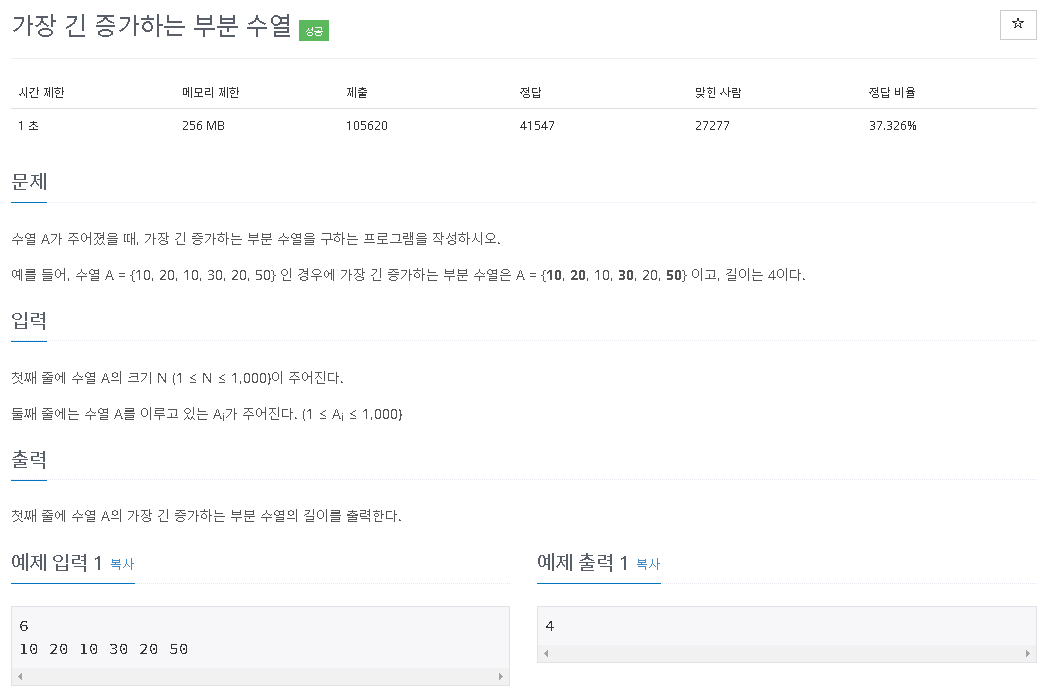
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
전형적인 LIS 문제이다. 하지만 역시 dp에 약한 나는 애를 먹었다...
문제를 읽고 처음 들었던 생각은, 수열의 i번째 값을 탐색할 경우 0 부터 i-1 값을 다 살펴보면 O(n^2) 으로 시간초과가 나지 않나? 하는 의문이었다. 게다가 i-1 과 i-2 만 살펴보는 피보나치와 달리 0 ~ i-1 을 매번 탐색하는 것은 dp 가 아니라고 생각했다.
결론적으로 O(n^2) 로 푸는 것이 맞고, 이 또한 점화식을 이용한 것이기에 dp가 맞다고 한다...
시간복잡도

본 문제에서 N의 범위가 (1 ≤ N ≤ 1,000) 이었기 때문에 O(N^2) 또한 1초 안에 가능하다.
| 0 | 1 | 2 | 3 | 4 | 5 | |
| arr[i] | 10 | 20 | 10 | 30 | 20 | 50 |
| dp[i] | 1 | 2 | 1 | 3 | 2 | 4 |
dp[0] = {10} : 길이 1
dp[1] = {10, 20} : 길이 2
dp[2] = {10} : 길이 1
dp[3] = {10, 20, 30} : 길이 3
dp[4] = {10, 20} : 길이 2
dp[5] = {10, 20, 30, 50} : 길이 4
class Main
{
public static void main(String args[]) throws Exception
{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
st=new StringTokenizer(br.readLine()," ");
int[] arr = new int[N];
int[] dp =new int[N];
for(int i=0;i<N;i++) {
arr[i]=Integer.parseInt(st.nextToken());
}
// LIS
for(int i=0;i<N;i++) {
dp[i]=1;
for(int j=0;j<N;j++) {
if(arr[j]<arr[i]&&dp[i]<dp[j]+1) {
dp[i]=dp[j]+1;
}
}
}
System.out.println(Arrays.stream(dp).max().getAsInt());
}
}
'알고리즘 > 문제 풀이' 카테고리의 다른 글
| [백준] 1149 : RGB거리 (JAVA) (0) | 2022.07.28 |
|---|---|
| [백준] 9663 : N-Queen (JAVA) (0) | 2022.07.28 |
| [백준] 11053 : 가장 긴 증가하는 부분 수열 / LIS (JAVA) (0) | 2022.07.28 |
| [백준] 1912 : 연속합 (JAVA) (0) | 2022.07.28 |
| [백준] 2805 : 나무 자르기 (JAVA) (0) | 2022.07.28 |




댓글